fvSchemes

foamSearch $FOAM_TUTORIALS fvSchemes ddtSchemes.default
foamSearch $FOAM_TUTORIALS fvSchemes gradSchemes
foamSearch $FOAM_TUTORIALS fvSchemes "divSchemes.div(phi,U)"
foamSearch $FOAM_TUTORIALS fvSchemes laplacianSchemes.default
foamSearch $FOAM_TUTORIALS fvSchemes interpolationSchemes.default
foamSearch $FOAM_TUTORIALS fvSchemes snGradSchemes

tree $FOAM_SRC/finiteVolume/finiteVolume/ddtSchemes -L 1
tree $FOAM_SRC/finiteVolume/finiteVolume/gradSchemes -L 1
tree $FOAM_SRC/finiteVolume/finiteVolume/divSchemes -L 1
tree $FOAM_SRC/finiteVolume/finiteVolume/laplacianSchemes -L 1
tree $FOAM_SRC/finiteVolume/finiteVolume/snGradSchemes -L 1

Time schemes example

Time schemes define how a property is integrated as a function of time

$\frac{\part}{\part t}(\phi)$

ddtSchemes
{
    default         backward;
    default         Crank-Nicolson 0.9; //for most condition [0 ~ 1]
    default         Euler;
    default         CoEuler phi rho 0.5;;
    default         SLTS phi rho 0.5;;
    default         Local Euler;
    default         steadyState;
    ddt(phi)        <time scheme>;
}
// if divSchemes using "bounded"
// ddtSchemes should define "bounded"
// default         bounded Euler;

Backward time scheme

Implicit
Second order
Transient
Boundedness not guaranteed
Conditionally stable

$\frac{\partial}{\partial t}(\phi)=\frac{1}{\Delta t}\left(\frac{3}{2} \phi-2 \phi^{o}+\frac{1}{2} \phi^{o o}\right)$

Crank-Nicolson time scheme

Second order
Transient
Bounded

$\frac{\partial}{\partial t}(\phi)=\frac{\phi-\phi^{o o}}{2 \Delta t}$

ddtSchemes
{
    default         CrankNicolson <coeff>
    ddt(phi)        CrankNicolson <coeff>;
}
// 0: Euler
// 1: Crank-Nicolson
// A value of 0.9 is a good compromise between accuracy and robustness
// CrankNicolson ocCoeff { type scale ; scale linearRamp ; duration 1 ; value 0.9 ; };

Euler implicit time scheme

Implicit
First order
Transient

$\frac{\partial}{\partial t}(\phi)=\frac{\phi-\phi^{o}}{\Delta t}$

Local Euler implicit/explicit time scheme

First order
Pseudo transient, designed for steady cases
Spatially varying, cell-based time scale set by specific Local Time Stepping (LTS) solvers

Steady state time scheme

Steady state
Sets temporal derivative contributions to zero

$\frac{\part}{\part t}(\phi)=0$

Interpolation schemes

Interpolation schemes are used to transform cell-centre quantities to face centres. The operation is used in many of the finite volume calculations, e.g. for the calculation of gradient, divergence, and Laplacian terms.

interpolationSchemes
{
    default         none;
    <equation term> <interpolation scheme>;
}

Linear divergence scheme

Second order
Unbounded
Good choice for LES calculations due to low dissipation
For isotropic meshes

$ϕ_f=0.5(ϕ_c+ϕ_d)$

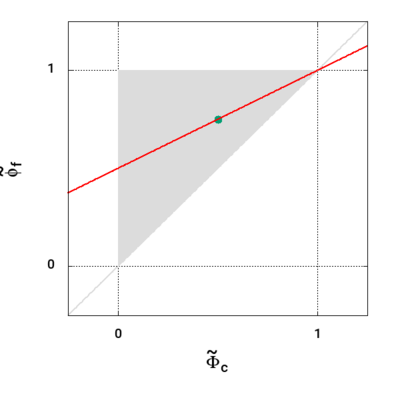
divSchemes
{
    default         none;
    div(phi,U)      Gauss linear;
    div(phi,U)      cubic;    // DNS case
}

Gradient schemes example

The gradient of a scalar property $\phi$ is represented using the notation:

$\nabla \phi=\mathbf{e}_{1} \frac{\partial}{\partial x_{1}} \phi+\mathbf{e}_{2} \frac{\partial}{\partial x_{2}} \phi+\mathbf{e}_{3} \frac{\partial}{\partial x_{3}} \phi$

gradSchemes
{
    default         none;
    grad(p)         <optional limiter> <gradient scheme> <interpolation scheme>;
}
// <limiters> cellLimited cellMDLimited faceLimited faceMDLimited clippedLinear
// <gradient scheme> fourth gauss leastSquares 
// <interpolation scheme> linear pointLinear leastSquares

Laplacian schemes

Taking the Laplacian of a property $ϕ$ is represented using the notation:

$\nabla^2 \phi= \frac{\partial ^2}{\partial x_{1}^2} \phi+ \frac{\partial ^2}{\partial x_{2}^2} \phi+ \frac{\partial ^2}{\partial x_{3}^2} \phi$

or as a combination of divergence and gradient operators

$\nabla \cdot(\Gamma \nabla \phi)$

where $Γ$ is a diffusion coefficient.

laplacianSchemes
{
    default         none;
    default         Gauss linear;
    default         Gauss linear corrected;
    default         Gauss linear corrected;
    default         Gauss linear corrected;
    laplacian(gamma,phi) Gauss <interpolation scheme> <snGrad scheme>
}

Divergence schemes example

The divergence of a property Q describes the net rate at which it changes as a function of space, represented using the notation:

$\nabla \cdot Q$

wallDist
{
    method meshWave;

    // Optional entry enabling the calculation
    // of the normal-to-wall field
    nRequired false;

    // Optional entry delaying wall distance update to every n steps
    // Default is 1 (update every step)
    updateInterval 5;
}

fvSchemes

Time schemes example

Interpolation schemes

Gradient schemes example

Laplacian schemes

Divergence schemes example